Chess Engine - (Part 1.5)

On scaling laws for Language Models

This is first in a series of blogs covering this project. TL;DR see this Github repo. Also for all you who do not understand the Indian number system just read this wiki. This is a follow up to my previous work where I train a language model on \(25Cr\) or \(225.1Mn\) moves and pose some questions.

If you have any freelancing work, contact me on my LinkedIn.

Initially this was going to be do and done kind of project but now it seems like this is going to take a while and if I am lucky I might just get a paper out of it. There are so many shitty papers out there that you can't believe something so meaningless can get a paper out. But anyways, it's them and we gotta do our योग. This blog is mostly a paper discussion and will be a quick one.

📶 What are power laws

It used to be when compute was low that simply adding more layers to a network used to work. But this paradigm changed with very large model (GPT-2, BERT, T5, etc.) and with the investment in these softwares it became important to know how these model actually scale, what matters and what not. So OpenAI did a research and answered those questions based on Power Law. So we start our discussion with what is a powerlaw.

Powerlaws are mathematical relationship where changing one value causes a proportional change in the outcome or power law is a function \(f(x)\) where the value \(y\) is proportional to some value of \(x\). Eg. doubling the length makes area \(4\) times and volume \(8\) times. So we can give it a form \(A(x) \propto x^k\) where \(k = 2\) and when considering volume \(k = 3\). Such functions have three properties:

  • Scale Invariance: given a relation \(f(x) = ax^{-\alpha}\) scaling \(x\) by a factor \(c\) causes proportional scaling of the function itself ie. \(f(cx) = c^{-\alpha} f(x)\). Thus the log of these values gives a linear line.
  • Lack of well defined average value, which makes it hard to apply traditional statistics like mean, etc. An example if the Pareto Distribution.
  • Universality, which in gist means that as a different systems behave the same way. And the exponent in such a distribution (\(k\)) remains the same for those different system. In the paper it means that for a lot of different models the scaling parameters eg. \(\alpha_N, \alpha_D\) remain the same for large number of values.

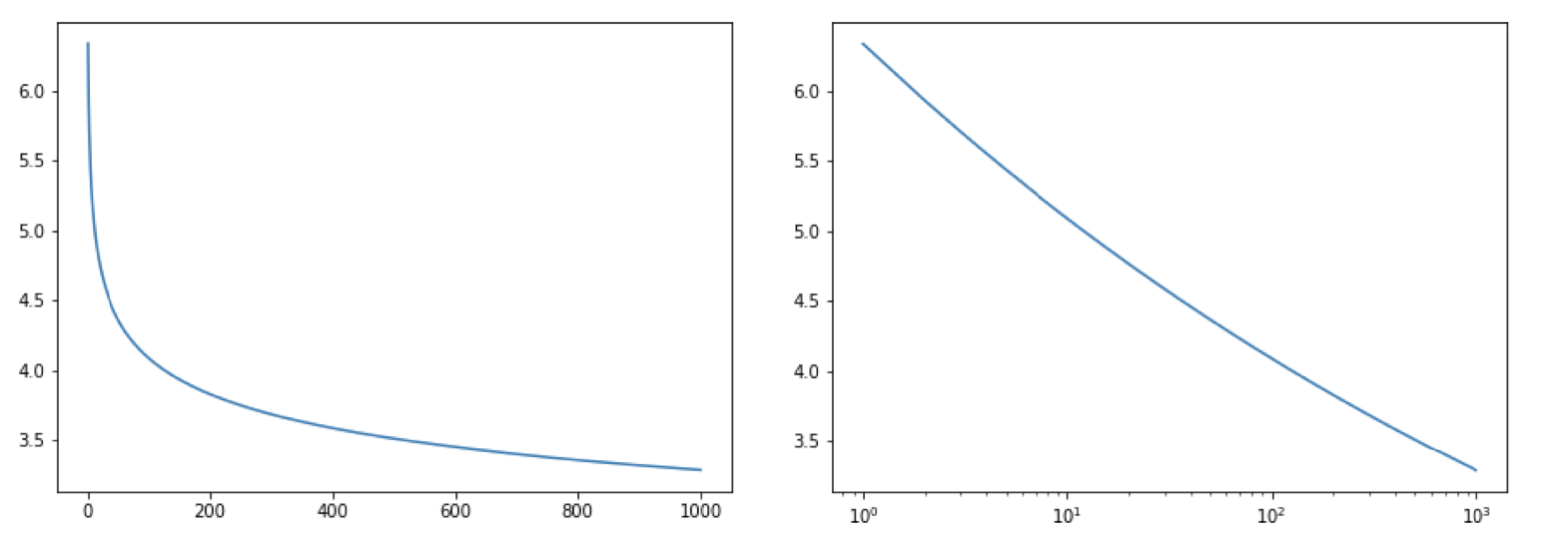
    (Left) you have normal power law distribution and (Right) shows that scaling x-axis to log gives a linear graph. Which helps when working exponentially increasing/decreasing values. \(y = f(x) = 5.6 x^{-0.095} \forall x \in [0,1000) \)

    📶 How to make network bigger (PROPERLY)

    The paper we are dealing with today is called "Scaling Laws for Neural Language Models" (ArXiv) by OpenAI. With the knowledge of the power laws it becomes easier to predict things at scale and this is helpful as neural networks grow exponentially in size. But we start with defining the nomenclature:

  • \(L\): Cross entropy loss in nats, typically it will be averaged over all the tokens in the context.
  • \(N\): The number of models parameters, excluding all the vocabulary and positional parameters. This can roughly be calculated as \(N \approx 2d_{model}n_{layer}(2 d_{attn} + d_{ff}) = 12n_{layer}d_{model}^2\)
  • \(D\): The dataset size in tokens
  • \(C\): Compute required. One forward pass takes \(C_{forward} \approx 2N + 2d_{model}n_{layer}n_{ctx}\) where the factor \(2\) comes from multiply-accumuate operation used in matrix multiplication. Accounting for the backwards pass (twice the forward pass) the total compute comes at \(C \approx 6N\) per training token.
  • \(B_{crit}\): The critical batch size. Training at the critical batch size provides a roughly optimize between time and compute efficiency.
  • \(C_{min}\): An estimate of the minimum amount of non-embedding compute to reach a given value of the loss (batch size \(\ll\) critical batch size)
  • \(S_{min}\): An estimate of the minimal number of training steps needed to reach a given value of the loss (batch size \(\ll\) critical batch size)
  • \(\alpha_X\): power law exponents for scaling of the loss \(L(X) \propto 1/X^{\alpha_X}\) where \(X\) can be any of \(N,D,C,S,B,C^{min}\)

    Parameter counts and compute (forward pass) estimates for a Transformer model. Sub-leading terms such as nonlinearities, biases, and layer normalization are omitted.

    What are the lesson learnt, those with images are given below the bullet points:

  • Transformer performance depends very weakly on the shape parameters \(n_{layer}, n_{heads}\) and \(d_{ff}\) when we hold the non-embedding parameters count fixed to \(N\).
  • The variation in the loss with different random seeds is roughly \(0.02\), does this mean setting seeds during training is pretty much useless?
  • To avoid overfitting when training within the above threshold of convergence we require \(D \geq (5 \times 10^3) N^{0.74}\). However, this according to my calculations actually comes \(D \geq (1.73 \times 10^3) N^{0.74}\) .
  • Convergence is inefficient: When working with a fixed compute \(C\) but without any other restrictions on \(N\) and \(D\), we attain optimal performance by training a very large network and stopping significantly before convergence. As given by relation \(D \sim C^{0.27}\)
  • The performance penalty depends predictably on the ratio \(N^{0.74}/D\), meaning that every time we increase the model size \(8\times\), we only need to increase the data by roughly \(5\times\) to avoid a penalty.
  • This is somewhat obvious but larger models are more sample efficient, reaching same performance with fewer parameters.

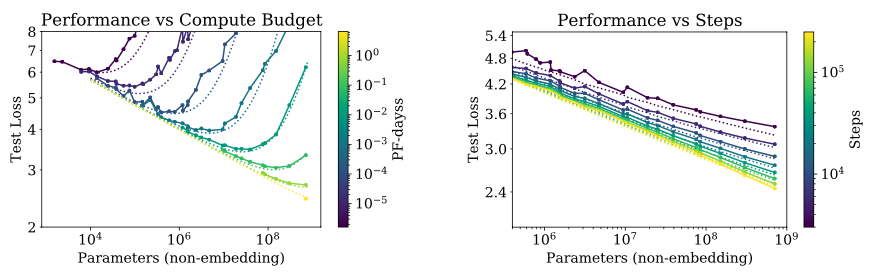
    (left) It means that for a given compute size there is an optimal model size (where the loss is lowest, on the line) and for the same amout of compute both the larger and the smaller models can give the same results (test loss). Thus we should find the optimal model for this compute size. (right) at same steps, larger models give lower loss and on increasing the steps there is decrease in loss for the same model.

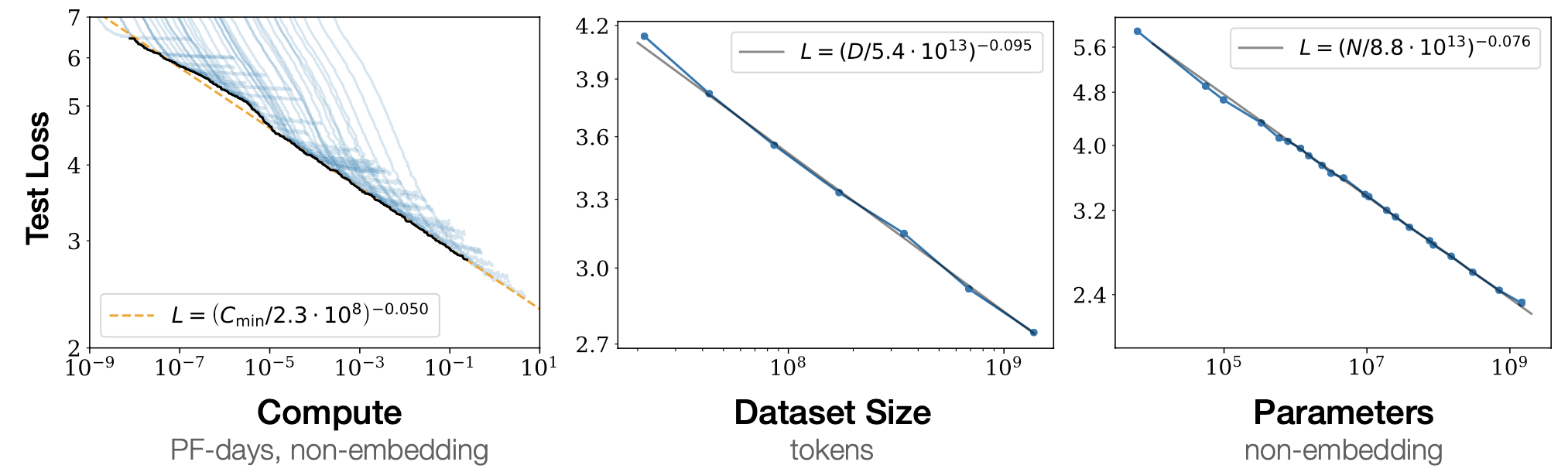
    This has to be the best representation of results. What this shows is that for each variable shown, if the other two are optimal then the test loss is very predictable and follows smooth curves. Thus in order to train an efficient model we need to grow all three in tandem. This is the engineering challenge!

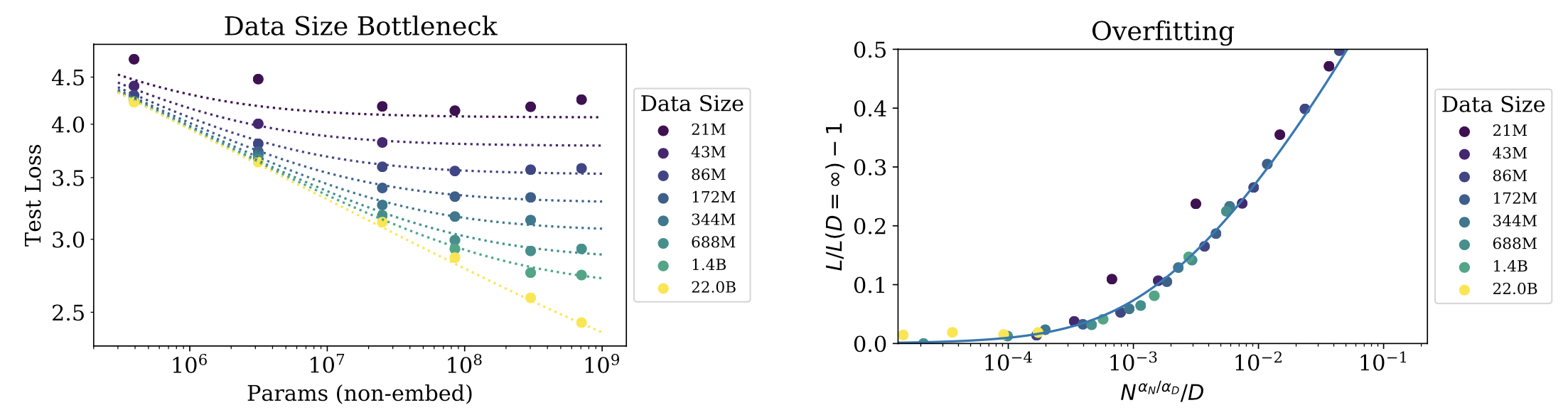
    This is another important graph. On the right you see that datasize can also become a bottleneck (😓 this sounds familiar), ie. when you have a small dataset even larger models can suffer same loss. When this happens no amount of compute or model size increase can help you and you start to move away from efficient frontier. On the right is the For reference: \(L(N,D) = \Big( (\frac{N_C}{N})^{\frac{\alpha_N}{\alpha_D}} + \frac{D_C}{D} \Big)^{\alpha_D}\) and on right, X-axis is \(N^{0.737}/D\).

    So what is the problem?

    Kolmogorov defined the complexity of a string \(\text{x}\) as the length of its shortest description \(\text{p}\) on a universal Turing machine \(\text{U(K(x))} = \min\{\text{l(p):U(p)=x}\}\), .